Отношение катетов это угол

Какие числа могут быть сторонами прямоугольного треугольника
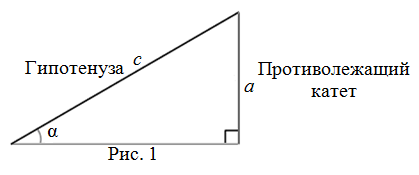
В прямоугольном треугольнике тригонометрические функции используются для вычисления сторон и острых углов треугольника. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Косинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.




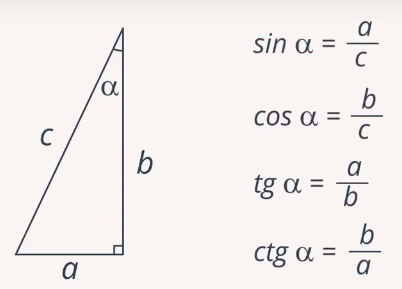




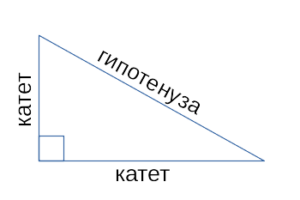
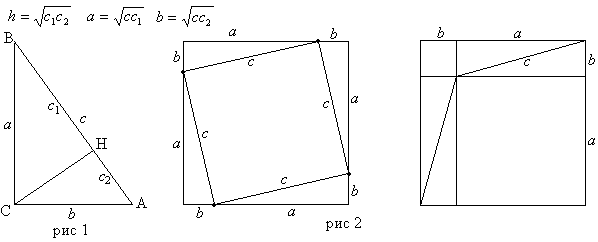
Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии. Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует, что в обозначениях, показанных на диаграмме: [1]. Кроме того, высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением: [2] [3]. Также если прямоугольный треугольник является равнобедренным , то высота, опущенная на гипотенузу будет равна:.
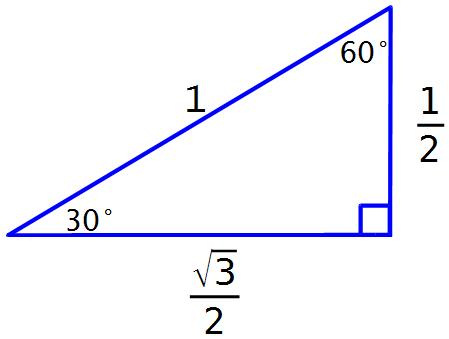
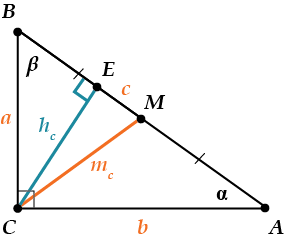
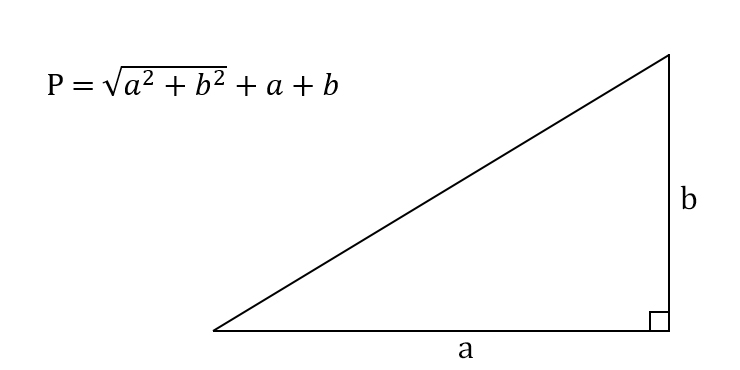
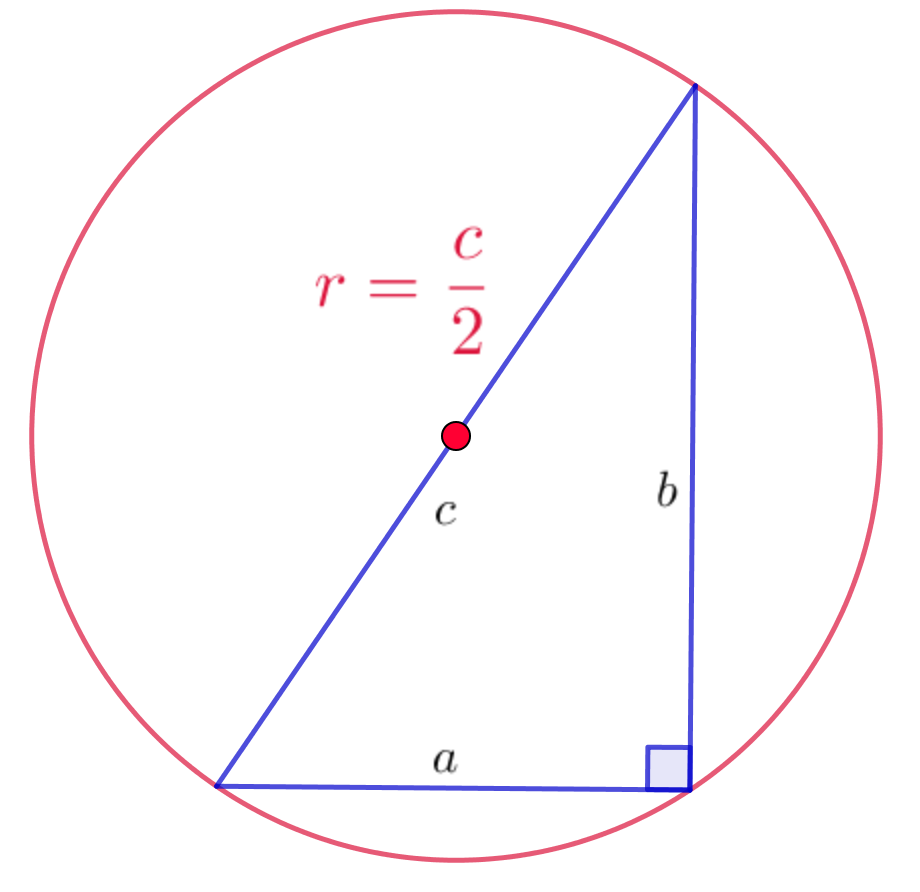
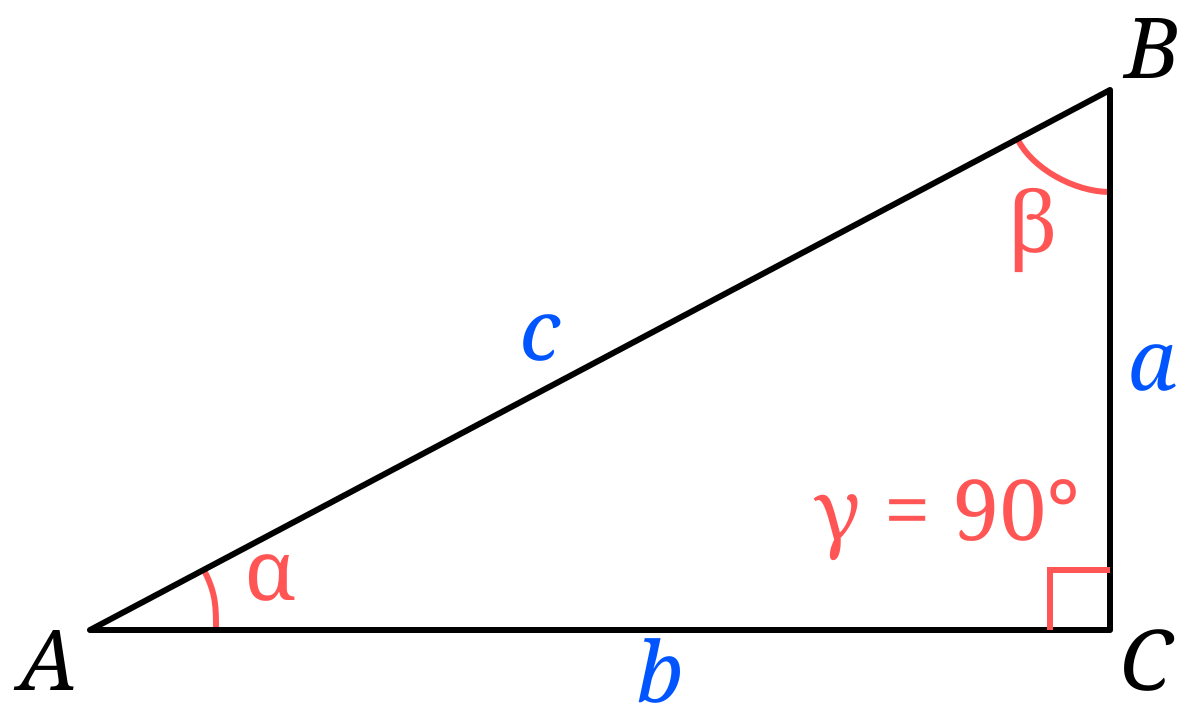




В геометрии одной из основных задач является определение соотношения длин двух катетов прямоугольного треугольника. Когда эти катеты находятся в соотношении 1 к 2, вопрос возникает о величине угла, образуемого этими сторонами. При соотношении катетов 1 к 2 угол между ними будет прямым. Это свойство прямоугольных треугольников, которое можно получить из теоремы Пифагора. Теорема Пифагора гласит, что сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.